In machine learning, when there are too many features, it can cause several problems, such as:

• Overfitting
• Slower processing speed
• Difficulty in visualizing if there are more than three features

Therefore, it is necessary to perform dimensionality reduction on the features. In practice, manually selecting features from hundreds or thousands of options is not a wise approach. So, let's introduce two commonly used dimensionality reduction methods in machine learning.

PCA (Principal Component Analysis)

Before introducing PCA, let's define our objective:

Transform a sample with n-dimensional feature space into a sample with k-dimensional feature space, where k < n.

The main steps of PCA are as follows:

1. Standardize the data.
2. Build the covariance matrix.
3. Use Singular Value Decomposition (SVD) to obtain eigenvectors and eigenvalues.
4. Usually, the eigenvalues are arranged in descending order. Select k eigenvalues and corresponding eigenvectors.
5. Project the original data onto the eigenvectors to obtain new feature values.

The most important part of PCA is Singular Value Decomposition. Now, let's talk about Singular Value Decomposition.

Intuitive Understanding of Singular Value Decomposition

Singular Value Decomposition is a well-known method in matrix decomposition. In high school mathematics, matrix decomposition is most commonly used to solve equations (such as LU decomposition). From the formula of Singular Value Decomposition, we can intuitively understand:

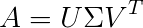
Here, A is an m x n matrix, U and V are orthogonal matrices, and Σ is the singular value matrix. The singular value matrix represents the eigenvalues of matrix A and is also called the principal components in PCA. It represents the importance of preserving information. The eigenvalues are usually arranged in descending order on the diagonal and form a symmetric matrix.

What does A correspond to in this case? It corresponds to our features. However, it is important to note that in PCA, we usually use the covariance matrix to perform Singular Value Decomposition. Remember to normalize the data before performing Singular Value Decomposition.

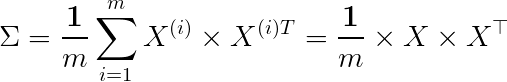
Covariance matrix

Since the covariance matrix is commonly denoted as Sigma (do not confuse it with Σ above), we can use the first k columns of U multiplied by the corresponding eigenvectors in Σ to obtain new features. From a geometric perspective:

In this geometric operation, X is projected onto the first k vectors of U.

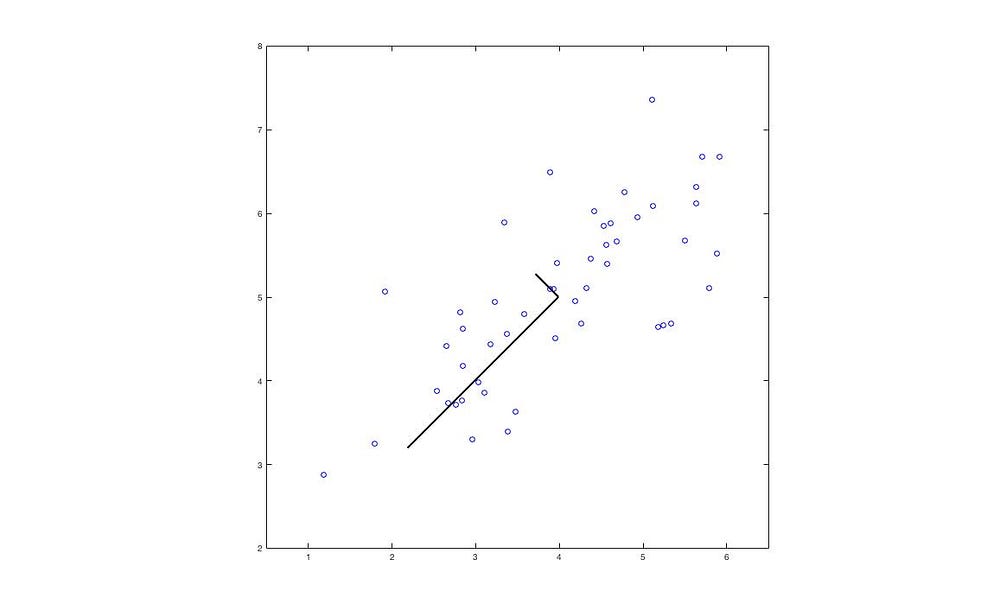
The black lines represent the eigenvectors, and their lengths represent the eigenvalues.

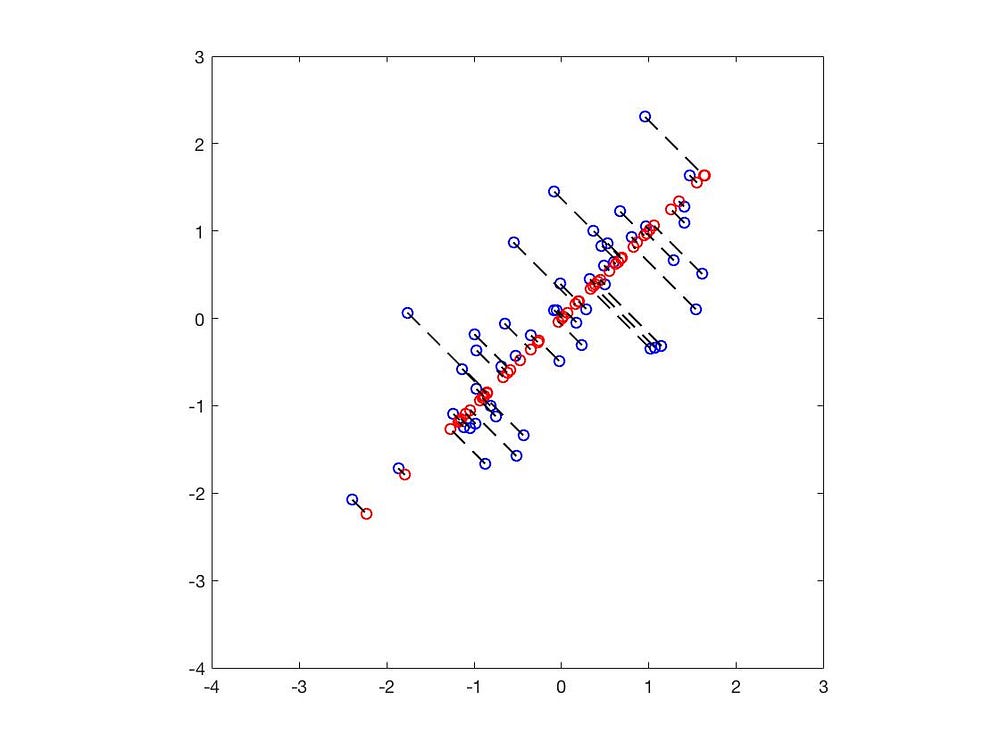
The blue dots represent the original data points, and the red dots represent the projected points on the eigenvectors. By doing this, we have successfully reduced the 2-dimensional data to 1-dimensional.

Of course, we can also reduce from 3-dimensional to 2-dimensional:

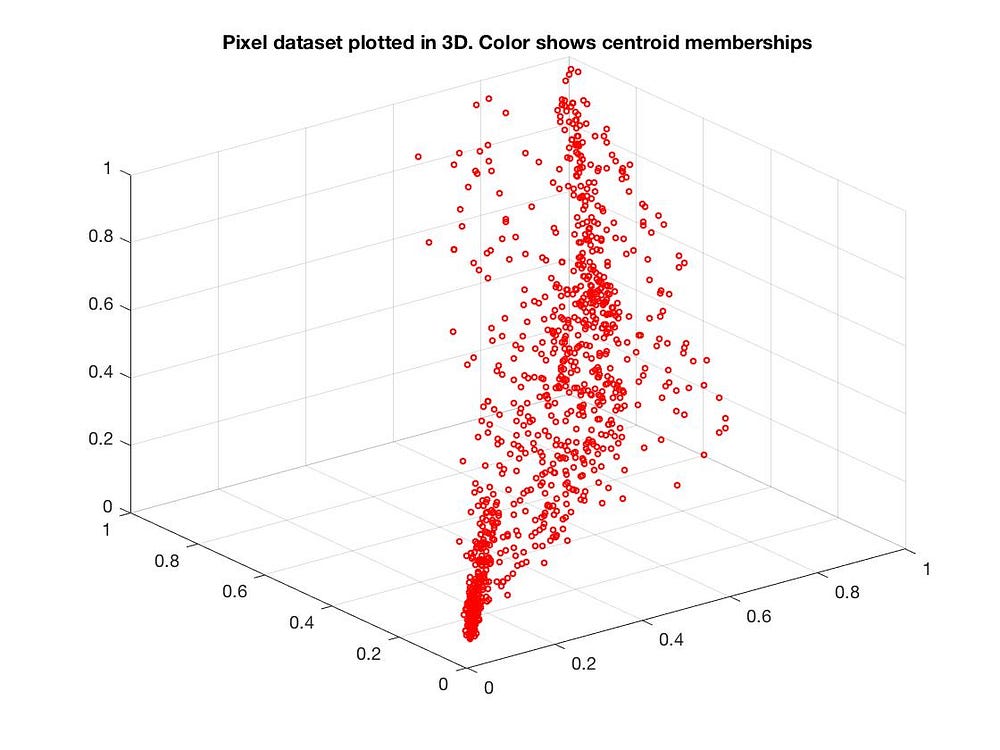
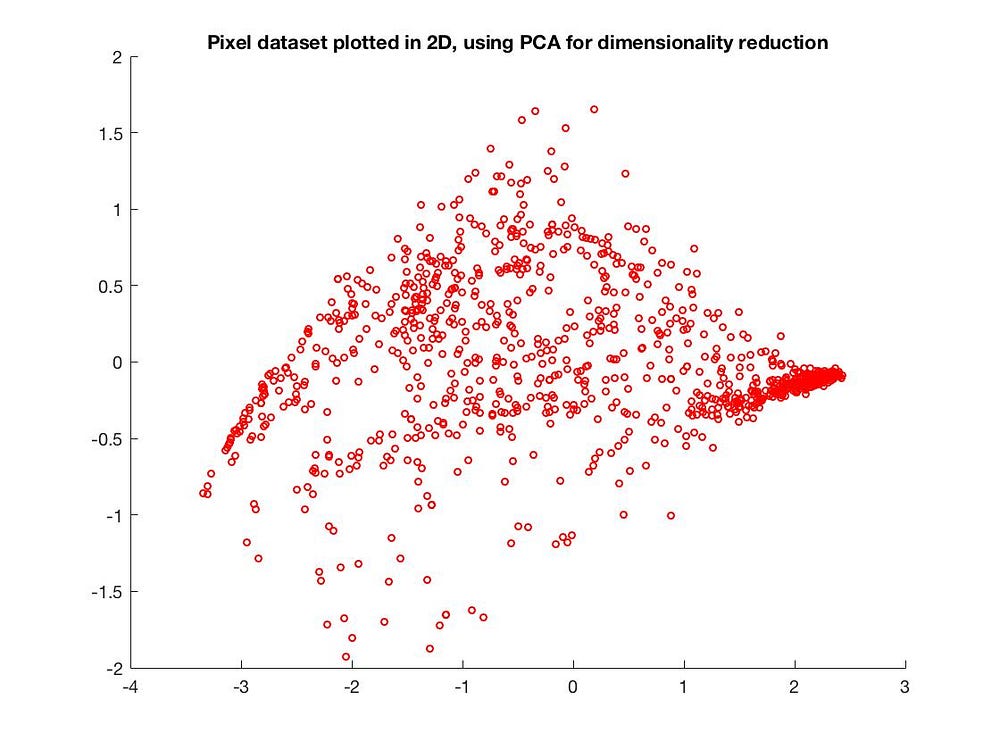
Applications of PCA

When performing dimensionality reduction, we want to keep the most important features and discard the less important ones.

For example, when judging a person, the most important distinguishing features might be the eyes, nose, and mouth. Therefore, we can discard features like skin color and hair, which are less important. In fact, PCA is commonly used in facial recognition for dimensionality reduction.

This provides a fairly intuitive understanding of Singular Value Decomposition. Due to space limitations, we cannot go into further detail. If you are interested in Singular Value Decomposition, you can refer to theWikipedia page.

t-SNE

PCA is a straightforward and effective method for dimensionality reduction. However, when we visualize the transformation from three dimensions to two dimensions, we can see that some clusters of data are completely mixed together.

PCA is a linear dimensionality reduction method, but if the relationships between features are nonlinear, using PCA may lead to underfitting.

t-SNE is another dimensionality reduction method that uses more complex formulas to express the relationship between high-dimensional and low-dimensional data. t-SNE approximates the high-dimensional data using Gaussian distributions and the low-dimensional data using t-distributions. It calculates similarity using KL divergence and finds the optimal solution using gradient descent (or stochastic gradient descent).

Gaussian Distribution - Probability Density Function

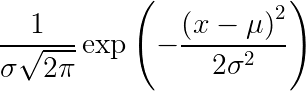
Here, X is a random variable, 𝝈 is the variance, and 𝜇 is the mean.

Thus, the original high-dimensional data can be represented as follows:

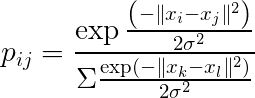
The low-dimensional data can be represented using the t-distribution's probability density function (with 1 degree of freedom):

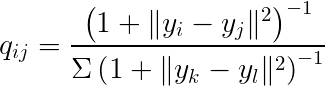
Here, x represents the high-dimensional data and y represents the low-dimensional data. P and Q represent probability distributions.

Why do we use the t-distribution to approximate the low-dimensional data? This is mainly because when transforming to a lower dimension, a lot of information is lost. To avoid being affected by outliers, the t-distribution is used.

The t-distribution is better at modeling the population distribution when the sample size is small and is less affected by outliers.

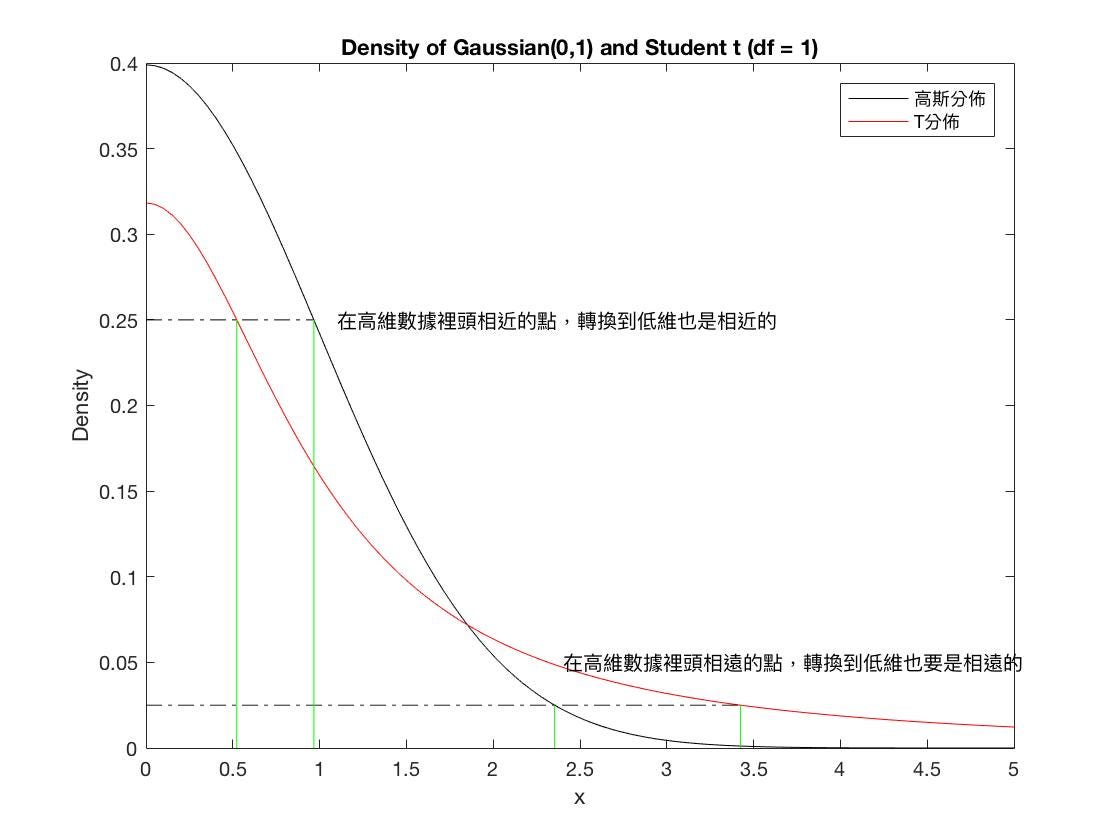Comparison of t-distribution and Gaussian distribution's probability density functions

Similarity Between the Two Distributions

The similarity between two distributions is often measured using KL divergence (Kullback-Leibler Divergence), also known as relative entropy.

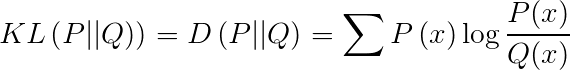
In t-SNE, perplexity is often used as a hyperparameter.

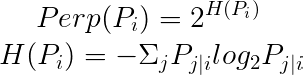
The paper suggests that perplexity is usually between 5 and 50.

Cost Function

The cost is calculated using KL divergence:

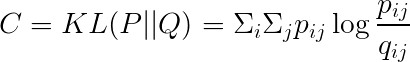
The gradient can be calculated as:

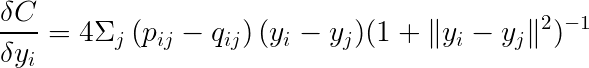
Finally, gradient descent (or stochastic gradient descent) is used to find the minimum.

Experiment: Testing with MNIST

You can download the test dataset here. Let's first reduce the dimensions to 2 using PCA.

PCA

PCA dimensionality reduction

After reducing the dimensions to 2 using PCA, we can see that the data is mixed together and it is difficult to distinguish clusters. This is because PCA's linear dimensionality reduction loses too much information.

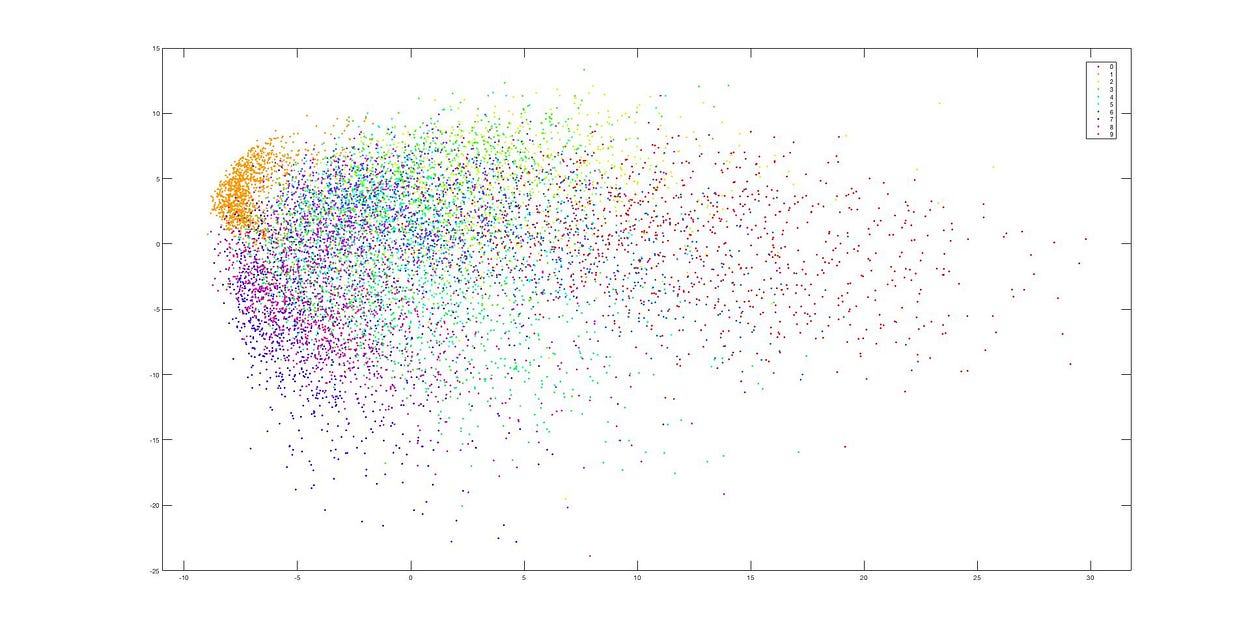
t-SNE

Next, let's test with t-SNE.

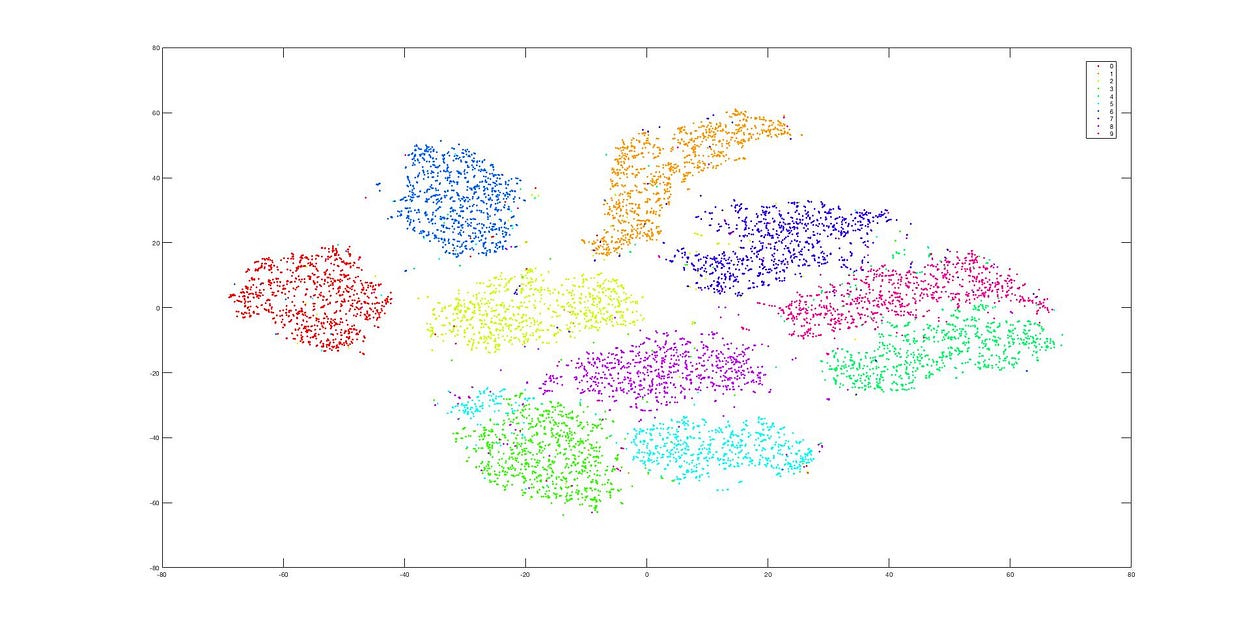t-SNE dimensionality reduction

This is the result after using t-SNE for dimensionality reduction. We can see that even after dimensionality reduction, the data is still clearly clustered. These two images clearly demonstrate the difference between PCA and t-SNE.

Conclusion

Later, there have been algorithms proposed to improve the performance of t-SNE. For more details, you can refer to the paper Accelerating t-sne using tree-based algorithms. Most popular data analysis programming languages, such as sklearn, R, and MATLAB, have implemented t-SNE.

However, t-SNE is not a linear dimensionality reduction method, so it takes more time to execute compared to PCA.

• When there are too many features, using PCA may result in underfitting. In such cases, t-SNE can be considered for dimensionality reduction.
• t-SNE requires more time to execute.
• The paper also discusses some optimization techniques (such as choosing perplexity), which will be covered gradually in the future.

References

• Van der Maaten, L., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research.
• Accelerating t-sne using tree-based algorithms. (2014). Retrieved from https://lvdmaaten.github.io/publications/papers/JMLR_2014.pdf
• 線代啟示錄 - 奇異值分解 (Singular Value Decomposition in Matrix Algebra)