還元法におけるPCAとT-Sneについての説明

機械学習において、特徴量が多すぎるといくつかの問題が発生する可能性があります。例えば：

• 過剰適合 (overfitting)
• 処理速度の低下
• 特徴量が三つ以上になると視覚化が難しい

このような場合、特徴量の次元を削減する必要があります。実務では、数百や数千の特徴量の中から手動で選択するのは明らかに賢明な方法ではありません。したがって、以下に機械学習でよく使用される二つの次元削減手法を紹介します。

PCA（主成分分析）

PCAを紹介する前に、まず私たちの目標を定義しましょう：

n個の特徴空間を持つサンプルを、k個の特徴空間を持つサンプルに変換する。ただし、k < nです。

以下はPCAの主なステップです：

1. データの標準化
2. **共分散行列（covariance matrix）**の作成
3. **特異値分解（SVD）を用いて固有ベクトル（eigenvector）と固有値（eigenvalue）**を求める
4. 通常、固有値は大きい順に並べてk個の固有値と固有ベクトルを選択する
5. 元のデータを固有ベクトルに投影（マッピング）して新しい特徴数を得る

PCAで最も重要な部分は特異値分解ですので、次の章では特異値分解について詳しく説明します。

特異値分解の直感的理解

行列分解の中で、特異値分解は非常に有名な方法です。行列分解は高校数学で最も一般的に使用される用途の一つで、方程式の解法（例えばLU分解）に用いられます。特異値分解の公式から、直感的に以下のように理解できます：

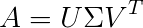
ここでAはm x nの行列で、𝑈とVは正規直交行列、𝛴は特異値行列です。特異値行列は行列Aに対応する固有値で、PCAでは主成分と呼ばれ、情報の保存の重要性を表します。通常、対角成分は大きい順に並び、対称行列です。

さて、このAは何に対応するのでしょうか？もちろん、私たちの特徴に対応します。ただし、ここでのAは通常**共分散行列（covariance matrix）**を使用して計算することに注意が必要です。データは必ず先に標準化してから特異値分解を行ってください。

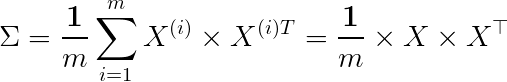
共分散行列（covariance matrix）

共分散行列は**シグマ（Σ）**で表されることが多いですが、上記の𝛴と混同しないようにしましょう。したがって、次元削減を行う際は、Uの前k列に対応する𝛴の固有ベクトルを掛けることで新しい特徴を得ることができます。幾何学的な観点から見ると、

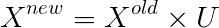
この計算は、幾何学的にはXをUの前k個のベクトルに投影することになります。

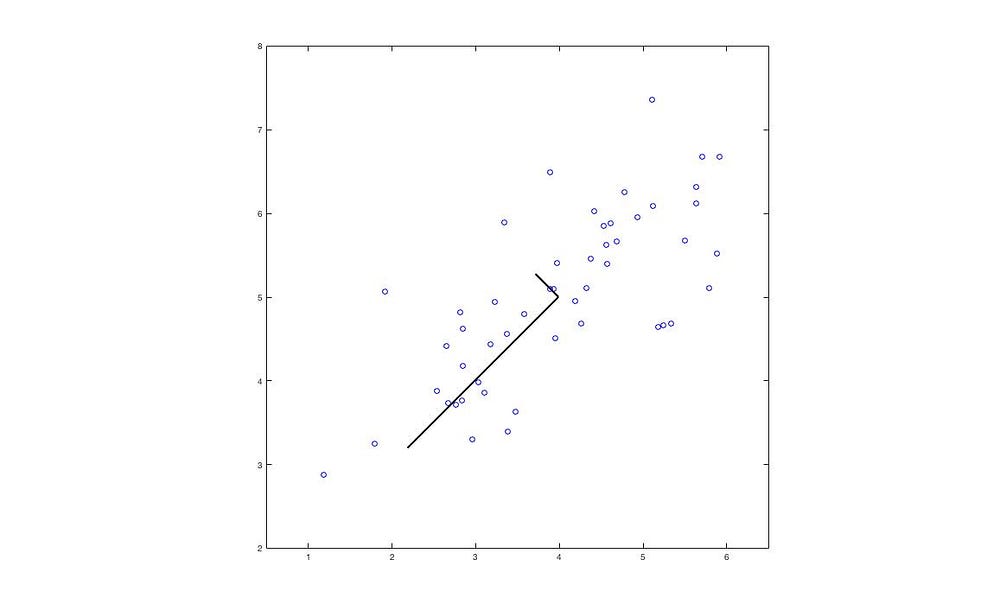
黒い線は固有ベクトルで、その長さは固有値を示します。

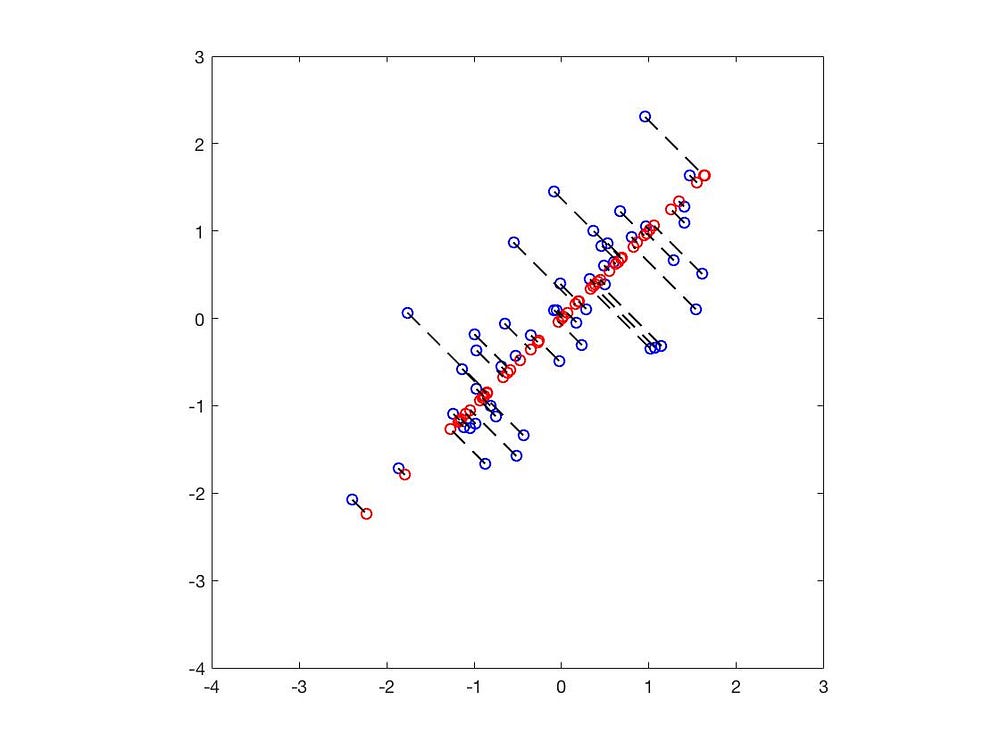
青い点は元のデータの位置を示し、赤い点は固有ベクトルに投影された位置です。これにより、2次元のデータを1次元に成功裏に削減しました。

もちろん、3次元から2次元への削減も可能です：

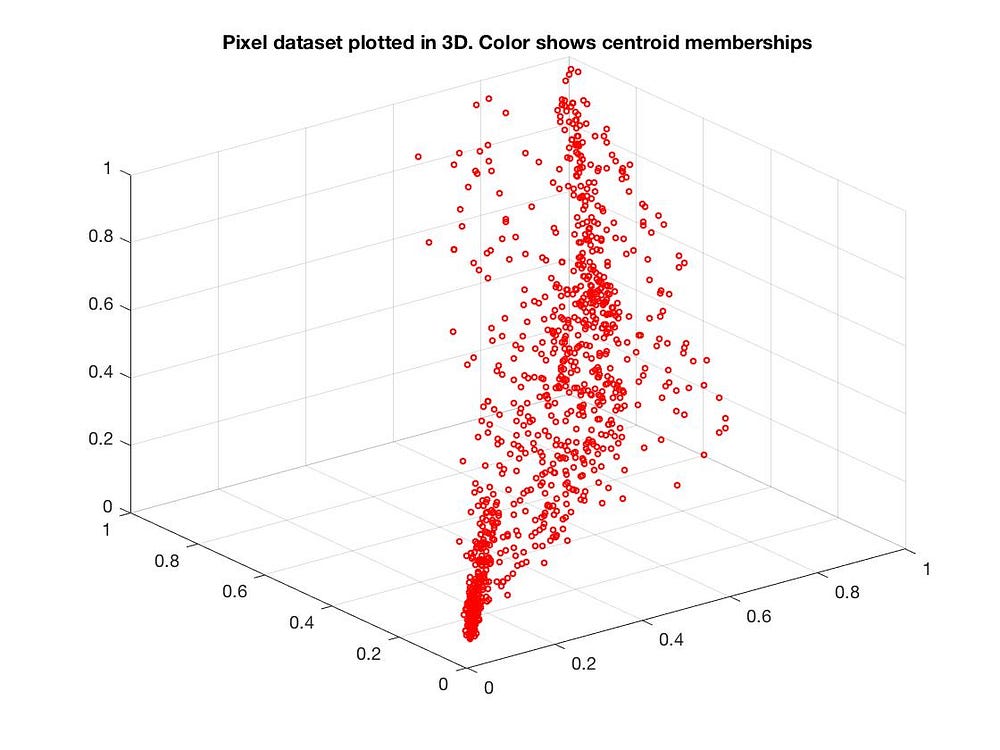
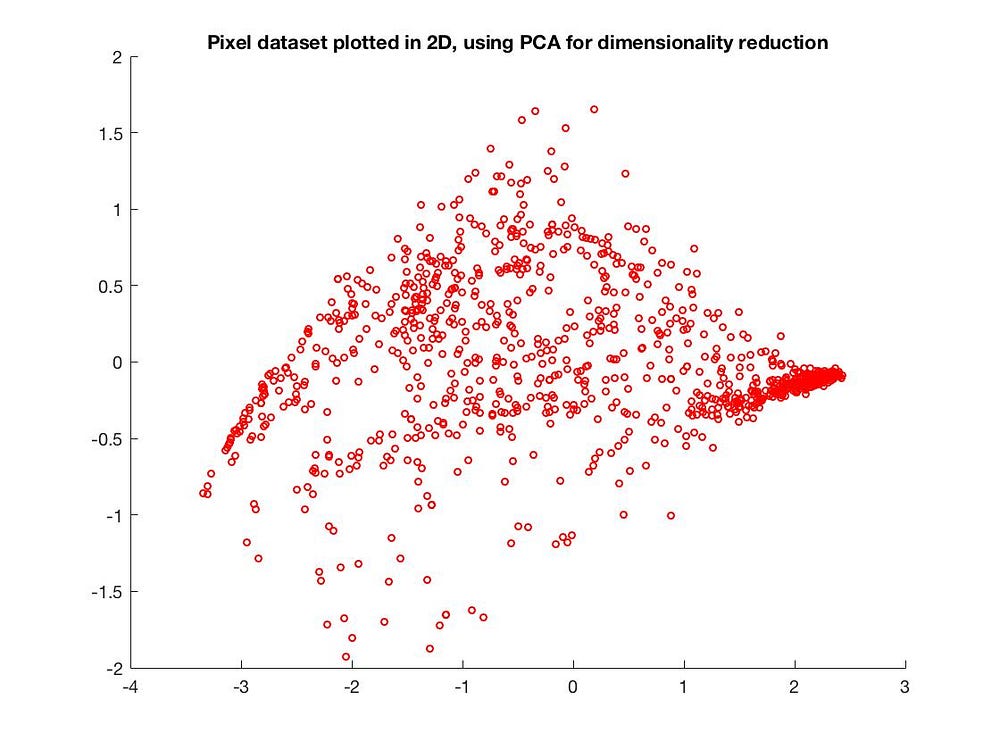
PCAの応用

次元削減を行う際には、最も重要な特徴を残したいと考えます。 残りの比較的重要でない特徴はそのまま捨てます。

例えば、人を判断する際、最も重要な判別要素は目、鼻、口などですので、肌の色や髪の毛などの特徴は捨てることができます。実際に顔認識でもPCAが次元削減に利用されることがよくあります。

これは特異値分解の非常に直感的な理解です。文章の長さの関係で詳細には触れられませんが、特異値分解に興味がある方はウィキペディアをご覧ください。

t-SNE

PCAは非常に直感的で効果的な次元削減方法ですが、三次元から二次元に変換する際、データのクラスタが完全に混ざり合ってしまうことが見受けられます。

PCAは線形次元削減の方法ですが、特徴間の関係が非線形の場合、PCAを使用すると**過少適合（underfitting）**を引き起こす可能性があります。

t-SNEも次元削減の一方法ですが、より複雑な公式を使用して高次元と低次元の関係を表現します。 t-SNEは主に、高次元データをガウス分布の確率密度関数で近似し、低次元データの部分はt分布を用いて近似します。KL距離で類似度を計算し、最後に勾配降下法（または確率的勾配降下法）で最適解を求めます。

ガウス分布の確率密度関数

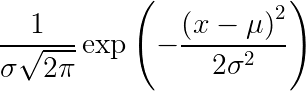
ここで、Xはランダム変数、𝝈は分散、𝜇は平均です。

したがって、元の高次元データは以下のように表現できます：

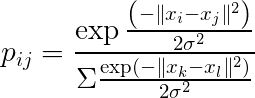
低次元データはt分布の確率密度関数で以下のように表現されます（自由度は1です）。

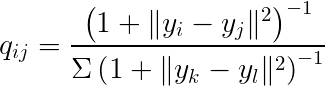
ここで、xは高次元のデータ、yは低次元のデータです。P、Qはそれぞれ確率分布を表します。

なぜ低次元データの近似にt分布を使用するのでしょうか？主な理由は、低次元に変換すると多くの情報が失われるため、外れ値の影響を受けにくくするためです。

t分布はサンプル数が少ないときに母集団分布の状況をより良く模擬でき、外れ値の影響を受けにくいのです。

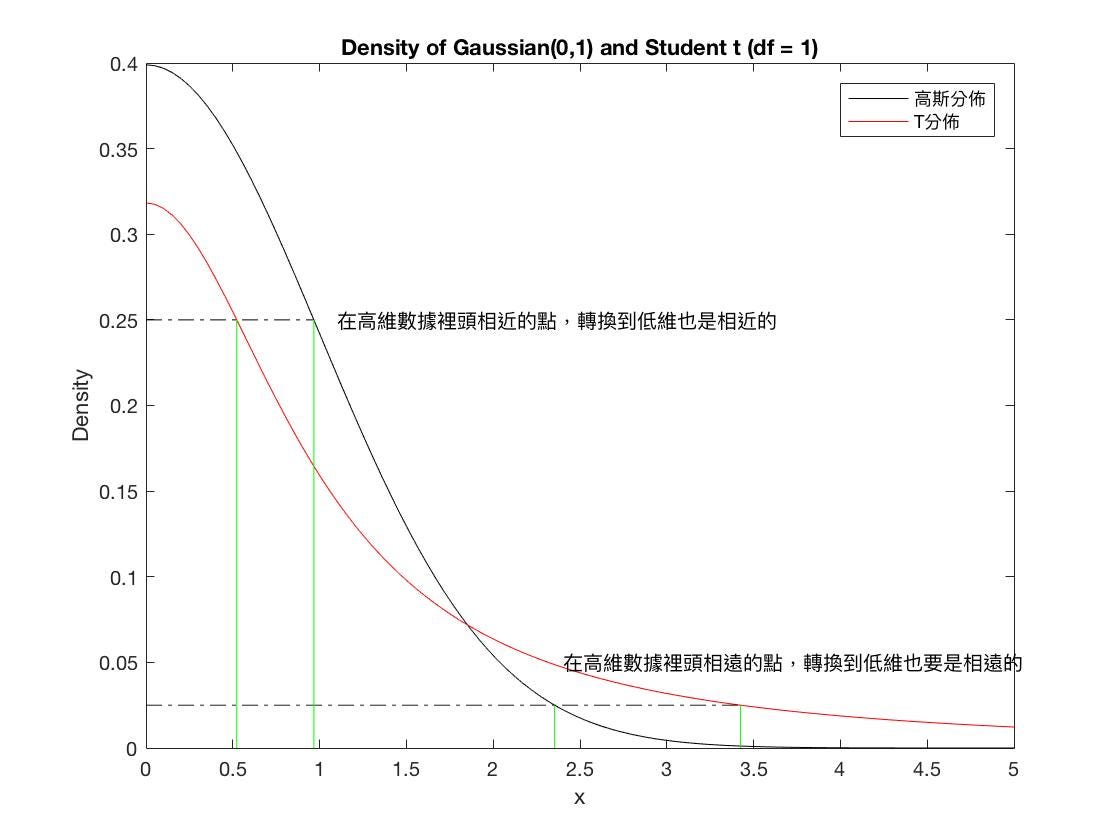T分布とガウス分布の確率密度関数

二つの分布間の類似度

二つの分布間の類似度を求めるために、KL距離（Kullback-Leibler Divergence）がよく使用され、相対エントロピー（Relative Entropy）とも呼ばれます。

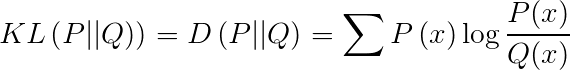
t-SNEでは、困惑度（Perplexity）がハイパーパラメータとして使用されます。

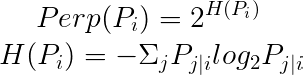
論文では、通常困惑度は5から50の間とされています。

コスト関数

KL距離を用いてコストを計算します。

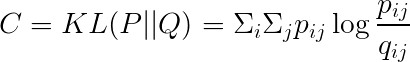
勾配は以下のように表現できます。

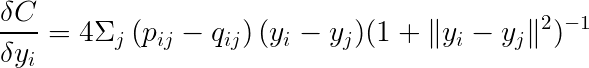
最後に勾配降下法（または確率的勾配降下法）を利用して最小値を求めることができます。

実測：MNISTを使用したテスト

テストデータセットはこちらからダウンロードできます。まず、PCAを用いて二次元に削減してみましょう。

PCA

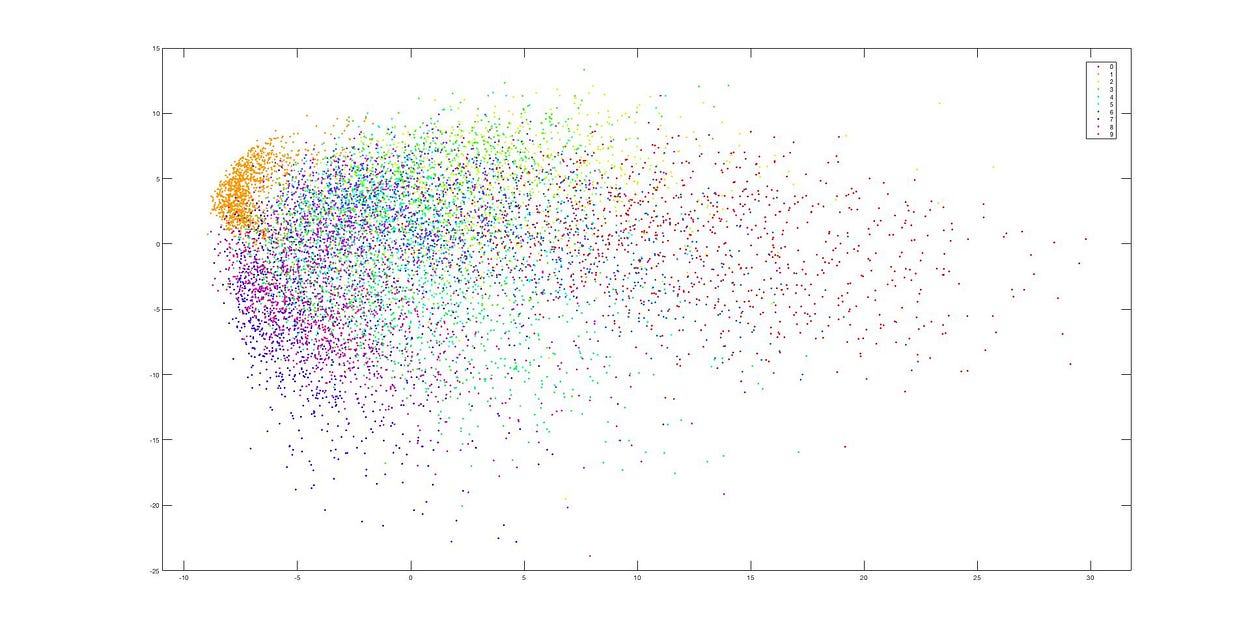PCAによる次元削減

二次元に削減した結果、データがほぼ一塊に混ざり合ってしまい、クラスタが全く見えなくなりました。これは、PCAの線形次元削減の過程で多くの情報が失われたためです。

t-SNE

次にt-SNEを使用してテストします。

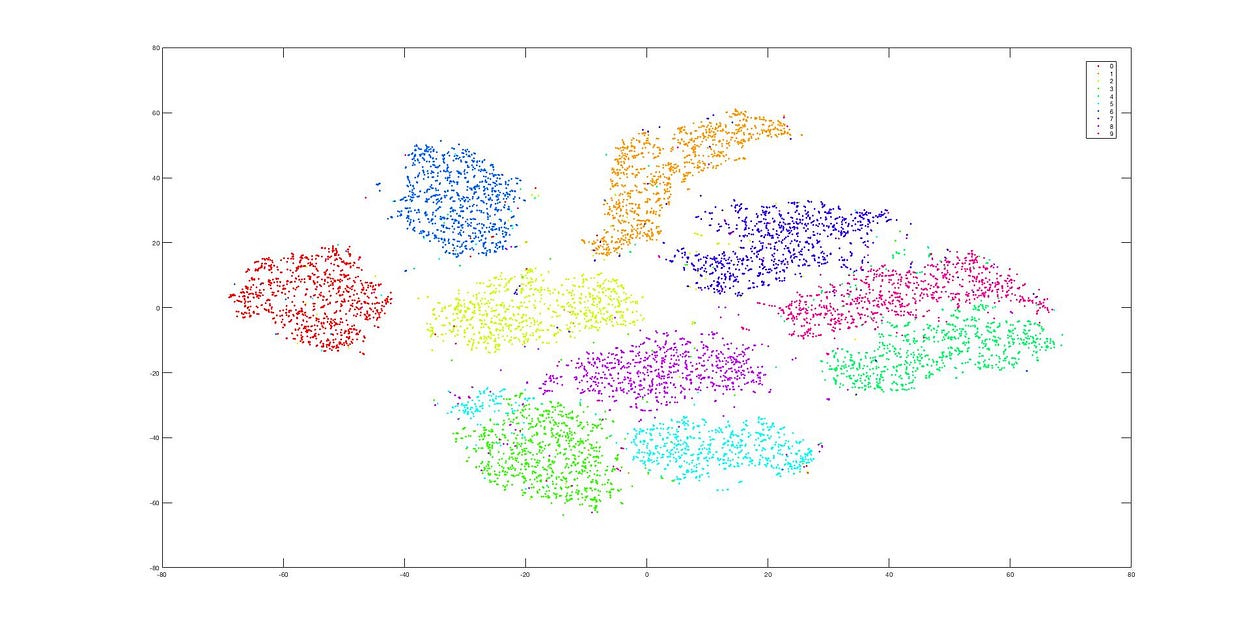t-SNEによる次元削減

これはt-SNEを使用した後の次元削減結果ですが、データが依然として非常に明確にクラスタ分けされています。これらの二つの図から、PCAとt-SNEの違いが非常に明確に分かります。

小結

その後、一連のt-SNEの性能を改善するアルゴリズムが提案されました。詳しくはAccelerating t-SNE using tree-based algorithmsを参照してください。多くの人気のあるデータ分析プログラミング言語でも実装されています。例えば、sklearnやR、MATLABなどです。

ただし、t-SNEは線形次元削減ではなく、実行時間はPCAよりもかなり長くなります。

• 特徴量が多すぎる場合、PCAを使用すると次元削減後の特徴が過少適合（underfitting）する可能性があります。この時、t-SNEを使用して次元削減を検討できます。
• t-SNEは実行に比較的多くの時間を要します。
• 論文には困惑度の選択など、いくつかの最適化技術がありますが、まだ完全には読み終えていないため、今後逐次補足していく予定です。

参考資料

• Van der Maaten L, Hinton G. Visualizing data using t-SNE
• Accelerating t-SNE using tree-based algorithms 各種ツリーアルゴリズムを利用してt-SNEの計算を加速する
• 線形代数の啓示 - 特異値分解

この記事はmediumにも同時に発表されています。